TL;DR Many real-world problems involving networks of transactions of various nature and social interactions and engagements are dynamic and can be modelled as graphs where nodes and edges appear over time. In this post, we describe Temporal Graph Network, a generic framework for deep learning on dynamic graphs.
This post was co-authored with Emanuele Rossi.
Graph neural networks (GNNs) research has surged to become one of the hottest topics in machine learning this year. GNNs have seen a series of recent successes in problems from the fields of biology, chemistry, social science, physics, and many others. So far, GNN models have been primarily developed for static graphs that do not change over time. However, many interesting real-world graphs are dynamic and evolving in time, with prominent examples including social networks, financial transactions, and recommender systems. In many cases, it is the dynamic behaviour of such systems that conveys important insights, otherwise lost if one considers only a static graph.
A dynamic graph can be represented as an ordered list or asynchronous “stream” of timed events, such as additions or deletions of nodes and edges [1]. A social network like Twitter is a good illustration to keep in mind: when a person joins the platform, a new node is created. When they follow another user, a follow edge is created. When they change their profile, the node is updated.
This stream of events is ingested by an encoder neural network that produces a time-dependent embedding for each node of the graph. The embedding can then be fed into a decoder that is designed for a specific task. One example task is predicting future interactions by trying to answer the question: what is the probability of having an edge between nodes i and j at time t? The ability to answer this question is crucial to recommendation systems that e.g. suggest social network users whom to follow or decide which content to display. The following figure illustrates this scenario:
The key piece in the above setup is the encoder that can be trained with any decoder. On the aforementioned task of future interaction prediction, the training can be done in a self-supervised manner: during each epoch, the encoder processes the events in chronological order and predicts the next interaction based on the previous ones [2].
Temporal Graph Network (TGN) is a general encoder architecture we developed at Twitter with colleagues Fabrizio Frasca, Davide Eynard, Ben Chamberlain, and Federico Monti [3]. This model can be applied to various problems of learning on dynamic graphs represented as a stream of events. In a nutshell, a TGN encoder acts by creating compressed representations of the nodes based on their interactions and updates them upon each event. To accomplish this, a TGN has the following main components:
Memory. The memory stores the states of all the nodes, acting as a compressed representation of the node’s past interactions. It is analogous to the hidden state of an RNN; however, here we have a separate state vector sᵢ(t) for each node i. When a new node appears, we add a corresponding state initialised as a vector of zeros. Moreover, since the memory for each node is just a state vector (and not a parameter), it can also be updated at test time when the model ingests new interactions.
Message Function is the main mechanism of updating the memory. Given an interaction between nodes i and j at time t, the message function computes two messages (one for i and one for j) , which are used to update the memory. This is analogous to the messages computed in message-passing graph neural networks [4]. The message is a function of the memory of nodes i and j at the instance of time t⁻ preceding the interaction, the interaction time t, and the edge features [5]:
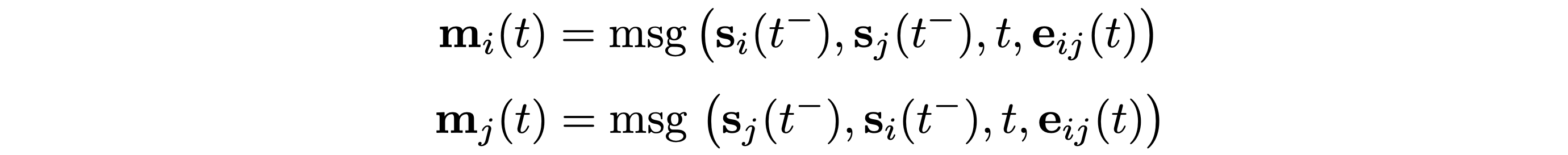
Memory Updater is used to update the memory with the new messages. This module is usually implemented as an RNN.

Given that the memory of a node is a vector updated over time, the most straightforward approach is to use it directly as the node embedding. In practice, however, this is a bad idea due to the staleness problem: given that the memory is updated only when a node is involved in an interaction, a long period of inactivity of a node causes its memory to go out of date. As an illustration, think of a user staying off Twitter for a few months. When the user returns, they might have already developed new interests in the meantime, so the memory of their past activity is no more relevant. We therefore need a better way to compute the embeddings.
Embedding. A solution is to look at the node neighbours. To solve the staleness problem, the embedding module computes the temporal embedding of a node by performing a graph aggregation over the spatiotemporal neighbours of that node. Even if a node has been inactive for a while, it is likely that some of its neighbours have been active, and by aggregating their memories, TGN can compute an up-to-date embedding for the node. In our example, even when a user stays off Twitter, their friends continue to be active, so when they return, the friends’ recent activity is likely to be more relevant than the user’s own history.
The overall computations performed by TGN on a batch of training data are summarised in the following figure:
By looking at the above diagram, you may be wondering how the memory-related modules (Message function, Message aggregator, and Memory updater) are trained, given that they seem not to directly influence the loss and therefore do not receive a gradient. In order for these modules to influence the loss, we need to update the memory before predicting the batch interactions. However, that would cause leakage, since the memory would already contain information about what we are trying to predict. The strategy we propose to get around this problem is to update the memory with messages coming from previous batches, and then predict the interactions. The diagram below shows the flow of operations of TGN, which is necessary to train the memory-related modules:
Inextensive experimental validation on various dynamic graphs, TGN significantly outperformed competing methods [6] on the tasks of future edge prediction and dynamic node classification both in terms of accuracy and speed. One such dynamic graph is Wikipedia, where users and pages are nodes, and an interaction represents a user editing a page. An encoding of the edit text is used as interaction features. The task in this case is to predict which page a user will edit at a given time. We compared different variants of TGN with baseline methods:
This ablation study sheds light on the importance of different TGN modules and allowing us to make a few general conclusions. First, the memory is important: its absence leads to a large drop in performance [7]. Second, the use of the embedding module (as opposed to directly outputting the memory state) is important. Graph attention-based embedding appears to perform the best. Third, having the memory makes it sufficient to use only one graph attention layer (which drastically reduces the computation time), since the memory of 1-hop neighbours gives the model indirect access to 2-hop neighbours information.
Asa concluding remark, we consider learning on dynamic graphs an almost virgin research area, with numerous important and exciting applications and a significant potential impact. We believe that our TGN model is an important step towards advancing the ability to learn on dynamic graphs consolidating and extending previous results. As this research field develops, better and bigger benchmarks will become essential. We are now working on creating new dynamic graph datasets and tasks as part of the Open Graph Benchmark.
[1] This scenario is usually referred to as “continuous-time dynamic graph”. For simplicity, here we consider only interaction events between pairs of nodes, represented as edges in the graph. Node insertions are considered as a special case of new edges when one of the endpoints is not presently in the graph. We do not consider node- or edge deletions, implying that the graph can only grow over time. Since there may be multiple edges between a pair of nodes, technically speaking, the object we have is a multigraph.
[2] Multiple interactions can have the same timestamp, and the model predicts each one of them independently. Moreover, mini-batches are created by splitting the ordered list of events in contiguous chunks of a fixed size.
[3] E. Rossi et al. Temporal graph networks for deep learning on dynamic graphs (2020). arXiv:2006.10637.
[4] For simplicity, we assume the graph to be undirected. In case of a directed graph, two distinct message functions, one for sources and one for destinations, would be needed.
[5] J. Gilmer et al. Neural Message Passing for Quantum Chemistry (2017). arXiv:1704.01212.
[6] There are only a handful of methods for deep learning on dynamic graphs, such as TGN of D. Xu et al. Inductive representation learning on temporal graphs (2020), arXiv:2002.07962 and Jodie of S. Kumar et al. Predicting dynamic embedding trajectory in temporal interaction networks (2019), arXiv:1908.01207. We show that the methods can be obtained as particular configurations of TGN. For this reason, TGN appears to be the most general model for learning on dynamic graphs so far. Earlier works considered dynamic knowledge graphs, e.g. A. García-Durán et al. Learning sequence encoders for temporal knowledge graph completion (2018). Proc. EMNLP.
[7] While the memory contains information about all past interactions of a node, the graph embedding module has access only to a sample of the temporal neighbourhood (for computational reasons) and may therefore lack access to information critical for the task at hand.
The authors are grateful to Giorgos Bouritsas, Ben Chamberlain, and Federico Monti for proof-reading this post, and to Stephan Günnemann for referring to earlier works on dynamic knowledge graphs.