How Do Artificial Neural Networks Learn?
This is the fifth post (Post 1, Post 2, Post 3, Post 4) in the series that I am writing based on the book First contact with DEEP LEARNING, Practical introduction with Keras. In it I will present an intuitive vision of the main components of the learning process of a neural network and put into practice some of the concepts presented here with an interactive tool called TensorFlow Playground.
Learning process of a neural network
Remember that a neural network is made up of neurons connected to each other; at the same time, each connection of our neural network is associated with a weight that dictates the importance of this relationship in the neuron when multiplied by the input value.
Each neuron has an activation function that defines the output of the neuron. The activation function is used to introduce non-linearity in the modeling capabilities of the network. We have several options for activation functions that we will present in this post.
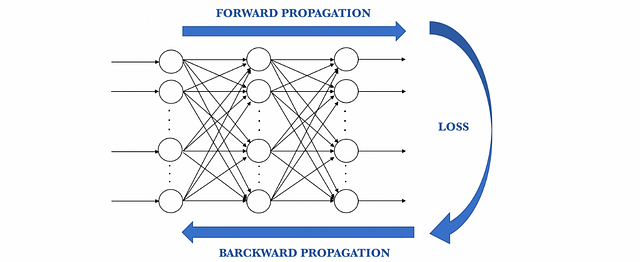
Training our neural network, that is, learning the values of our parameters (weights wij and bj biases) is the most genuine part of Deep Learning and we can see this learning process in a neural network as an iterative process of “going and return” by the layers of neurons. The “going” is a forwardpropagation of the information and the “return” is a backpropagation of the information.
The first phase forwardpropagation occurs when the network is exposed to the training data and these cross the entire neural network for their predictions (labels) to be calculated. That is, passing the input data through the network in such a way that all the neurons apply their transformation to the information they receive from the neurons of the previous layer and sending it to the neurons of the next layer. When the data has crossed all the layers, and all its neurons have made their calculations, the final layer will be reached with a result of label prediction for those input examples.
Next, we will use a loss function to estimate the loss (or error) and to compare and measure how good/bad our prediction result was in relation to the correct result (remember that we are in a supervised learning environment and we have the label that tells us the expected value). Ideally, we want our cost to be zero, that is, without divergence between estimated and expected value. Therefore, as the model is being trained, the weights of the interconnections of the neurons will gradually be adjusted until good predictions are obtained.
Once the loss has been calculated, this information is propagated backwards. Hence, its name: backpropagation. Starting from the output layer, that loss information propagates to all the neurons in the hidden layer that contribute directly to the output. However, the neurons of the hidden layer only receive a fraction of the total signal of the loss, based on the relative contribution that each neuron has contributed to the original output. This process is repeated, layer by layer, until all the neurons in the network have received a loss signal that describes their relative contribution to the total loss.
Visually, we can summarize what we have explained with this visual scheme of the stages:
Now that we have spread this information back, we can adjust the weights of connections between neurons.What we are doing is making the loss as close as possible to zero the next time we go back to using the network for a prediction. For this, we will use a technique called gradient descent. This technique changes the weights in small increments with the help of the calculation of the derivative (or gradient) of the loss function, which allows us to see in which direction “to descend” towards the global minimum; this is done in general in batches of data in the successive iterations (epochs) of all the dataset that we pass to the network in each iteration.
To recap, the learning algorithm consists of:
- Start with values (often random) for the network parameters (wij weights and bj biases).
- Take a set of examples of input data and pass them through the network to obtain their prediction.
- Compare these predictions obtained with the values of expected labels and calculate the loss with them.
- Perform the backpropagation in order to propagate this loss to each and every one of the parameters that make up the model of the neural network.
- Use this propagated information to update the parameters of the neural network with the gradient descent in a way that the total loss is reduced and a better model is obtained.
- Continue iterating in the previous steps until we consider that we have a good model.
Returning to the figure in a previous post which visually summarizes the learning process of one perceptron in a general way, these stages would be reflected in this way:
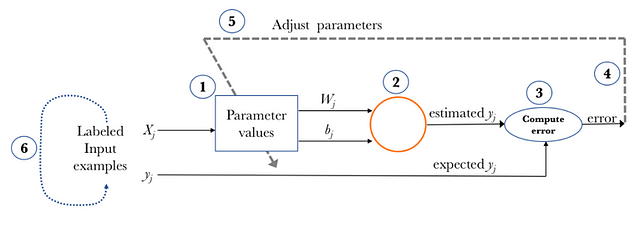
Below we present in more detail each of the elements that we have highlighted in this section.
Activation functions
Remember that we use the activation functions to propagate the output of a neuron forward. This output is received by the neurons of the next layer to which this neuron is connected (up to the output layer included). As we have said, the activation function serves to introduce non-linearity in the modeling capabilities of the network. Below we will list the most used nowadays; all of them can be used in a layer of Keras (we can find more information on their website).
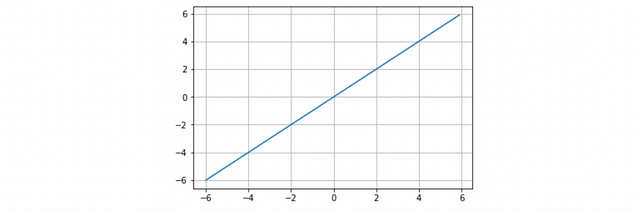
Linear
The linear activation function is basically the identity function in which, in practical terms, it means that the signal does not change.
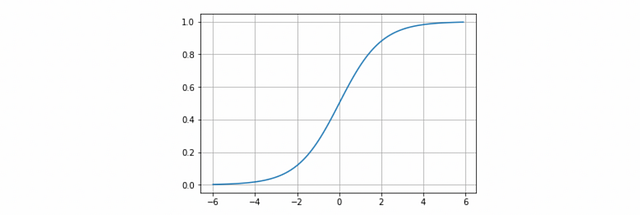
Sigmoid
The sigmoid function has already been introduced in a previous post. Its interest lies in the fact that it allows a reduction in extreme or atypical values in valid data without eliminating them: it converts independent variables of almost infinite range into simple probabilities between 0 and 1. Most of its output will be very close to the extremes of 0 or 1.
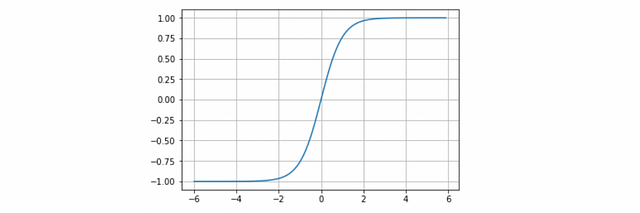
Tanh
Without going into detail, we can summarize that the tanh represents the relationship between the hyperbolic sine and the hyperbolic cosine: tanh(x)=sinh(x)/cosh(x). Unlike the sigmoid function, the normalized range of tanh is between -1 and 1, which is the input that goes well with some neural networks. The advantage of tanh is that negative numbers can be dealt with more easily.
Softmax
The softmax activation function was also presented in a previous post to generalize the logistic regression, insofar as instead of classifying in binary it can contain multiple decision limits. As we have seen, the softmax activation function will often be found in the output layer of a neural network and return the probability distribution over mutually exclusive output classes.
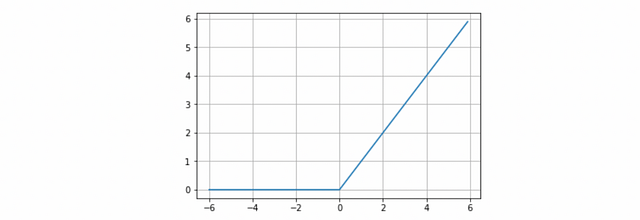
ReLU
The activation function rectified linear unit (ReLU) is a very interesting transformation that activates a single node if the input is above a certain threshold. The default and more usual behavior is that, as long as the input has a value below zero, the output will be zero but, when the input rises above, the output is a linear relationship with the input variable of the form f(x)=x. The ReLU activation function has proven to work in many different situations and is currently widely used.
Backpropagation components
In summary, we can consider backpropagation as a method to alter the parameters (weights and biases) of the neural network in the right direction. It starts by calculating the loss term first, and then the parameters of the neural network are adjusted in reverse order with an optimization algorithm taking into account this calculated loss.
Remember that in Keras the compile() method allows us to define how we want the components that are involved in the learning process to be:
Specifically, in this example, three arguments are passed to the method: an optimizer, a loss function, and a list of metrics. In classification problems like our example, accuracy is used as a metric. Let’s go a little deeper into these arguments.
Loss function
A loss function is one of the parameters required to quantify how close a particular neural network is to the ideal weight during the training process.
In the Keras manual page, we can find all types of loss functions available. Some have their concrete hyperparameters that must be indicated; in the example of the previous post, when we use categorical_crossentropy as a function of loss, our output must be in a categorical format. The choice of the best function of loss resides in understanding what type of error is or is not acceptable for the problem in particular.
Optimizers
The optimizer is another of the arguments required in the compile() method. Keras currently has different optimizers that can be used: SGD, RMSprop, Adagrad, Adadelta, Adam, Adamax, Nadam. You can find more detail about each of them in the Keras documentation.
In general, we can see the learning process as a global optimization problem where the parameters (weights and biases) must be adjusted in such a way that the loss function presented above is minimized. In most cases, these parameters cannot be solved analytically, but in general they can be approached well with iterative or optimizing optimization algorithms, such as those mentioned above.
Gradient descent
We will explain one of the concrete optimizers so that you understand the overall operation of the optimizers. Specifically, the gradient descent, the basis of many optimizers and one of the most common optimization algorithms in Machine Learning and Deep Learning.
Gradient descent uses the first derivative (gradient) of the loss function when updating the parameters. Remember that the gradient gives us the slope of a function at that point. Without being able to go into detail, the process consists in chaining the derivatives of the loss of each hidden layer from the derivatives of the loss of its upper layer, incorporating its activation function in the calculation (that’s why the activation functions must be derivable). In each of the iterations, once all the neurons have the value of the gradient of the loss function that corresponds to them, the values of the parameters are updated in the opposite direction to that indicated by the gradient. The gradient, in fact, always points in the direction in which the value of the loss function increases. Therefore, if the negative of the gradient is used, we can get the direction in which we tend to reduce the loss function.
Let’s see the process in a visual way assuming only one dimension: suppose that this line represents the values that the loss function takes for each possible parameter value and that the negative of the gradient is depicted by the arrow in the initial point:
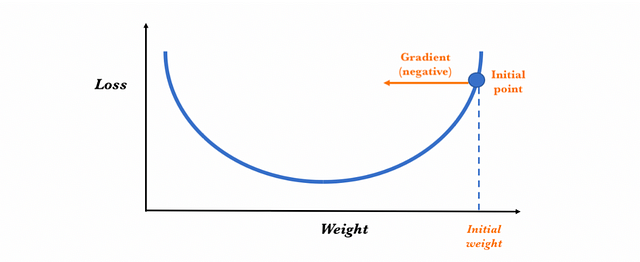
To determine the next value for the parameter, the gradient descent algorithm modifies the value of the initial weight to go in the opposite way to the gradient (since it points in the direction in which the loss grows and we want to reduce it), adding a proportional amount to this. The magnitude of this change is determined by the value of the gradient and by a learning rate hyperparameter that we can specify (which we will present shortly). Therefore, conceptually, it is as if we follow the slope downhill until we reach a local minimum:
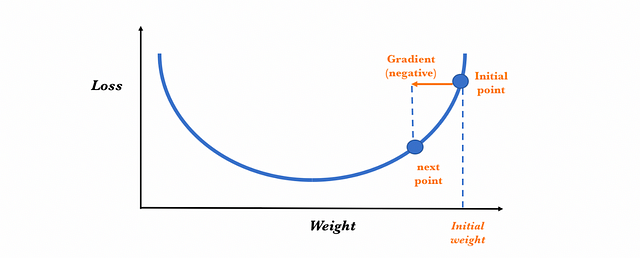
The gradient descent algorithm repeats this process getting closer and closer to the minimum until the value of the parameter reaches a point beyond which the loss function cannot decrease:
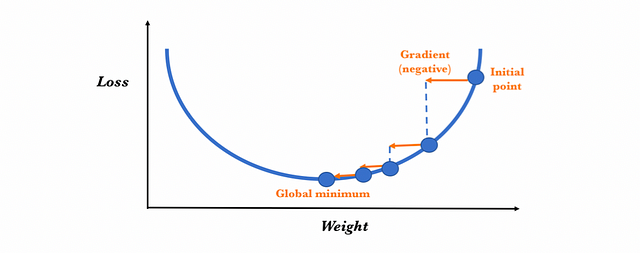
Stochastic Gradient Descent (SGD)
In the previous sections we have seen how the values of the parameters are adjusted but not in what frequency:
- After each entry example?
- After each round of the whole set of training examples (epoch)?
- After a sample of examples of the training set?
In the first case we speak of online learning, when the gradient is estimated from the observed loss for each example of the training; it is also when we talk about Stochastic Gradient Descent (SGD). The second is known as batch learning and is called Batch Gradient Descent. The literature indicates that, usually, better results can be obtained with online learning, but there are reasons that justify the use of batch learning because many optimization techniques only work with it.
But if the data is well distributed, a small subset of them should give us a pretty good approximation of the gradient. We may not get the best estimate, but it is faster and, given the fact that we are iterating, this approach is very useful. For this reason, the third aforementioned option known as mini-batch is often used. This option is usually as good as the online, but fewer calculations are required to update the parameters of the neural network. In addition, the simultaneous calculation of the gradient for many input examples can be done using matrix operations that are implemented very efficiently with GPU, as we have seen in a previous post.
That’s why, in reality, many applications use the stochastic gradient descent (SGD) with a mini-bach of several examples. To use all the data, what is done is to partition the data in several batches. Then we take the first batch, go through the network, calculate the gradient of its loss and update the parameters of the neural network; this would follow successively until the last batch. Now, in a single pass through all the input data, only a number of steps have been made equal to the number of batches.
SGD is very easy to implement in Keras. In the compile() method it is indicated that the optimizer is SGD (value sgd in the argument), and then all that must be done is to specify the batch size in the training process with the fit()method as follows :
model.fit(X_train, y_train, epochs=5, batch_size=100)
In this code example that uses the fit() method, we are dividing our data into batches of 100 with the batch_size argument. With the number of epochs we are indicating how many times we carry out this process on all the data. Later in this post, when we have already presented the usual optimizer parameters, we will return to these two arguments.
Model parameterization
If the reader at the end of the previous post has executed a model with the hyperparameters that we use there, I assume that the model’s accuracy will have exceeded 90%. Are these results good? I think they are fantastic, because it means that the reader has already programmed and executed his first neural network with Keras. Congratulations!
Another thing is that there are other models that improve accuracy. And this depends on having a great knowledge and a lot of practice to handle well with the many hyperparameters that we can change. For example, with a simple change of the activation function of the first layer, passing from a sigmoid to a relu like the one shown below:
model.add(Dense(10, activation=’relu’, input_shape=(784,)))
We can get 2% more accuracy with more or less the same calculation time.
It is also possible to increase the number of epochs, add more neurons in a layer or add more layers. However, in these cases, the gains in accuracy have the side effect of increasing the execution time of the learning process. For example, if we add 512 nodes to the intermediate layer instead of 10 nodes:
model.add(Dense(512, activation=’relu’, input_shape=(784,)))
We can check with the summary() method that the number of parameters increases (it is a fully connected) and the execution time is significantly higher, even reducing the number of epochs. With this model, the accuracy reaches 94%. And if we increase to 20 epochs, a 96% accuracy is achieved.
In short, an immense world of possibilities will be seen in more detail in the following section, where the reader can realize that finding the best architecture with the best parameters and hyperparameters of activation functions requires some expertise and experience given the multiple possibilities that we have.
Parameters and hyperparameters
So far, for simplicity, we have not paid explicit attention to differentiating between parameters and hyperparameters, but I think the time has come. In general, we consider a parameter of the model as a configuration variable that is internal to the model and whose value can be estimated from the data. In contrast, by hyperparameter we refer to configuration variables that are external to the model itself and whose value in general cannot be estimated from the data, and are specified by the programmer to adjust the learning algorithms.
When I say that Deep Learning is more an art than a science, I mean that it takes a lot of experience and intuition to find the optimal values of these hyperparameters, which must be specified before starting the training process so that the models train better and more quickly. Given the introductory nature of the book we will not go into detail about all of them, but we have hyperparameters that are worth mentioning briefly, both at the structure and topology level of the neural network (number of layers, number of neurons, their activation functions, etc.) and at the learning algorithm level (learning rate, momentum, epochs, batch size, etc.).
Next, we will introduce some of them and the rest will appear in a futuro post as we go into convolutional neural network.
Epochs
As we have already done, epochs tells us the number of times all the training data have passed through the neural network in the training process. A good clue is to increase the number of epochs until the accuracy metric with the validation data starts to decrease, even when the accuracy of the training data continues to increase (this is when we detect a potential overfitting).
Batch size
As we have said before, we can partition the training data in mini batches to pass them through the network. In Keras, the batch_size is the argument that indicates the size of these batches that will be used in the fit() method in an iteration of the training to update the gradient. The optimal size will depend on many factors, including the memory capacity of the computer that we use to do the calculations.
Learning rate
The gradient vector has a direction and a magnitude. Gradient descent algorithms multiply the magnitude of the gradient by a scalar known as learning rate (also sometimes called step size) to determine the next point.
In a more formal way, the backpropagation algorithm computes how the error changes with respect to each weight:
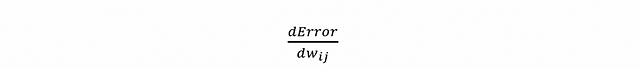
In order to update each weight of the network using a simple update rule:
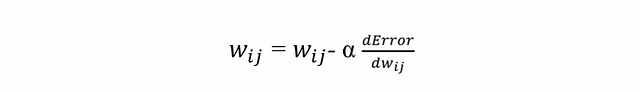
Where α is the learning rate.
For example, if the magnitude of the gradient is 1.5 and the learning rate is 0.01, then the gradient descent algorithm will select the next point at 0.015 from the previous point.
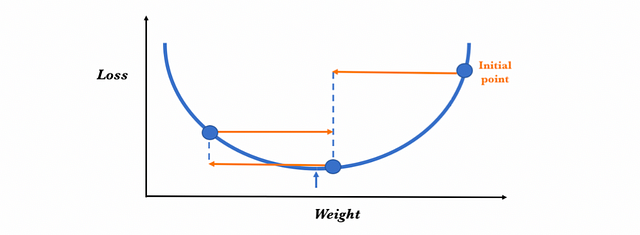
The proper value of this hyperparameter is very dependent on the problem in question, but in general, if this is too big, huge steps are being made, which could be good to go faster in the learning process. But in this case, we may skip the minimum and make it difficult for the learning process to stop because, when searching for the next point, it perpetually bounces randomly at the bottom of the “well”. Visually we can see in this figure the effect that can occur, where the minimum value is never reached (indicated with a small arrow in the drawing):
Contrarily, if the learning rate is small, small advances will be made, having a better chance of reaching a local minimum, but this can cause the learning process to be very slow. In general, a good rule is to decrease the learning rate if our learning model does not work. If we know that the gradient of the loss function is small, then it is safe to test that it compensates the gradient with the learning rate.
Learning rate decay
But the best learning rate in general is one that decreases as the model approaches a solution. To achieve this effect, we have another hyperparameter, the learning rate decay, which is used to decrease the learning rate as epochs go by to allow learning to advance faster at the beginning with larger learning rates. As progress is made, smaller and smaller adjustments are made to facilitate the convergence of the training process to the minimum of the loss function.
Momentum
In the visual example with which we have explained the descent gradient algorithm, to minimize the loss function we have the guarantee of finding the global minimum because there is no local minimum in which the optimization process can be stuck. However, in reality, the real cases are more complex and, visually, it is as if we could find several local minimums and the loss function had a form like the one in the following figure:
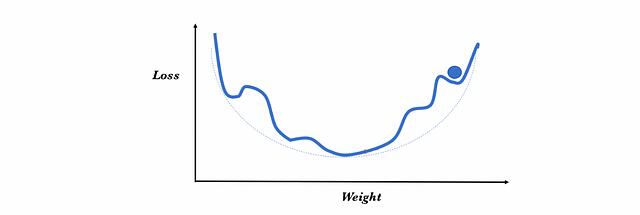
In this case, the optimizer can easily get stuck at a local minimum and the algorithm may think that the global minimum has been reached, leading to suboptimal results. The reason is that the moment we get stuck, the gradient is zero and we can no longer get out of the local minimum strictly following the path of the gradient.
One way to solve this situation could be to restart the process from different random positions and, in this way, increase the probability of reaching the global minimum.
To avoid this situation, another solution that is generally used involves the momentum hyperparameter. In an intuitive way, we can see it as if, to move forward, it will take the weighted average of the previous steps to obtain a bit of impetus and overcome the “bumps” as a way of not getting stuck in local minima. If we consider that the average of the previous ones was better, perhaps it will allow us to make the jump.
But using the average has proved to be a very drastic solution because, perhaps in gradients of previous steps, it is much less relevant than just in the previous one. That is why we have chosen to weight the previous gradients, and the momentum is a constant between 0 and 1 that is used for this weighting. It has been shown that algorithms that use momentum work better in practice.
One variant is the Nesterov momentum, which is a slightly different version of the momentum update that has recently gained popularity and which basically slows down the gradient when it is close to the solution.
Initialization of parameter weights
The initialization of the parameters’ weight is not exactly a hyperparameter, but it is as important as any of them and that is why we make a brief paragraph in this section. It is advisable to initialize the weights with small random values to break the symmetry between different neurons, if two neurons have exactly the same weights they will always have the same gradient; that supposes that both have the same values in the subsequent iterations, so they will not be able to learn different characteristics.
Initializing the parameters randomly following a standard normal distribution is correct, but it can lead to possible problems of vanishing gradients (when the values of a gradient are too small and the model stops learning or takes too long due to that) or exploding gradients (when the algorithm assigns an exaggeratedly high importance to the weights).
In general, heuristics can be used taking into account the type of activation functions that our network has. It is outside the introductory level of this book to go into these details but, if the reader wants to go deeper, I suggest that you visit the CS231n course website of Andrej Karpathy in Stanford, where you will obtain very valuable knowledge in this area exposed in a very didactic way.
Hyperparameters and optimizers in Keras
How can we specify these hyperparameters? Recall that the optimizer is one of the arguments that are required in the compile() method of the model. So far we have called them by their name (with a simple strings that identifies them), but Keras also allows to pass an instance of the optimizer class as an argument with the specification of some hyperparameters.
For example, the stochastic gradient descent optimizer allows the use of the momentum, learning rate decay and Nesterov momentum hyperparameters:
keras.optimizers.SGD(lr=0.01, momentum=0.0, decay=0.0,
nesterov=False)
The values indicated in the arguments of the previous method are those taken by default and whose range can be:
- lr: float >= 0. (learning rate)
- momentum: float >= 0
- decay: float >= 0 (learning rate decay).
- nesterov: boolean (which indicates whether or not to use Nesterov momentum).
As we have said, there are several optimizers in Keras that the reader can explore on their documentation page.
TensorFlow Playground
TensorFlow Playground is an interactive visualization web application written in JavaScript that allows us to simulate simple neural networks that run in our browser and see the results in real time:
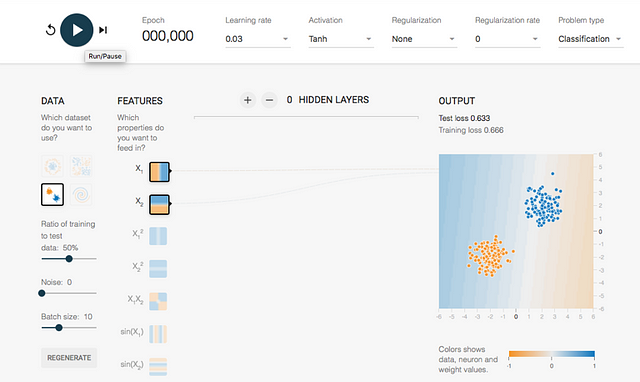
With this tool we can experiment with different hyperparameters and see their behavior. In fact, the flexibility provided by the hyperparameters in neural networks is one of its virtues and at the same time one of its drawbacks for those who start on the subject: there are many of them to adjust!
A binary classification problem
To begin to understand how the tool works we can use the first example of perceptron presented in a previous post, a simple classification problem.
To start with this example, we chose the dataset indicated in the “DATA” section shown in the previous figure, and then click on the “Play” button. Now we can see how TensorFlow Playground solves this particular problem. The line between the blue and orange area begins to move slowly. You can press the “Reset” button and re-test it several times to see how the line moves with different initial values.
In this case, the application tries to find the best values of the parameters that allow classifying these points correctly. If the cursor is put over the arcs, the reader will see that the value that has been assigned to each parameter appears (and it even allows us to edit it):

Remember that this weight dictates the importance of this relationship in the neuron when multiplying it by the input value.
After this first contact, we will present a little the tool that will allow us to understand how a neural network behaves. In the upper part of the menu, we basically find hyperparameters, some of which we already commented in the previous section: Epoch, Learning rate, Activation, Regularization rate, and Problem type. All of them are drop-down menus in which we can choose the value of these hyperparameters.
In the “Problem type” tab, the platform allows us to specify two types of problems: Regression (continuous problem) and Classification. In total, there are four types of data that we can choose for classification and two types for regression:
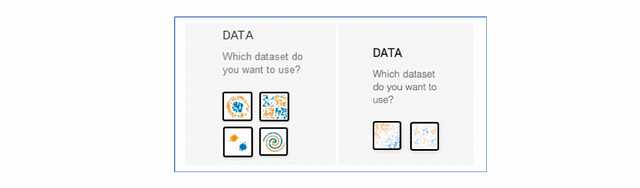
The blue and orange dots form the dataset. The orange points have the value -1 and the blue points the value +1. On the left side, below the data type, there are different parameters that we can modify to tune our input data.
Using the tab “Ratio of training to test data” we can control the percentage of data that is assigned to the training set (if we modify it we see how the points that appear in the “OUTPUT” on the right side of the screen are changed interactively). The noise level of the data can also be defined and controlled by the “Noise” field; the data pattern becomes more irregular as the noise increases. As we can experience, when the noise is zero, the problem data are clearly distinguished in their regions. However, when reaching more than 50, we can see that the blue dots and the orange dots are mixed, so it is very difficult to classify them.
With “Batch size”, as its name suggests, we can determine the amount of data that will be used for each training batch.
Then, in the next column, we can make the selection of features. I propose that we use “X1” and “X2” among the many available to us: “X1” is a value on the horizontal axis, and “X2” is the value on the vertical axis.
The topology of the neuronal network can be defined in the following column. We can have up to six hidden layers (by adding hidden layers, by clicking on the “+” sign) and we can have up to eight neurons per hidden layer (by clicking on the “+” sign of the corresponding layer):
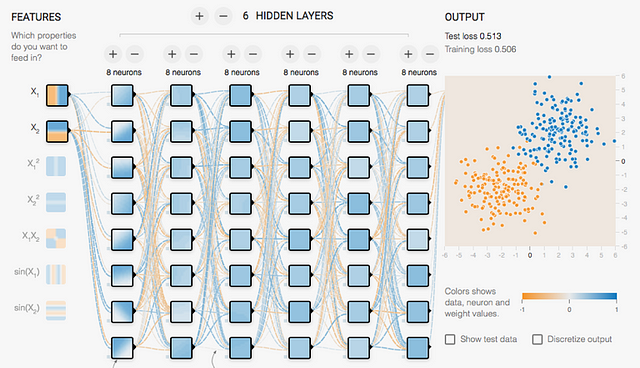
Finally, remember that when training the neural network we want to minimize the “Training loss” and then compare that with the test data the “Test loss” is also minimized. The changes of both metrics in each epoch are shown interactively in the upper right part of the screen, in a small graph where, if the loss is reduced, the curve goes downwards. The loss test is painted in black, and the training loss is painted in gray.
Hyperparameter setting basics
Classification with a single neuron
Now that we know a bit more about this tool, let’s return to the first classification example that separates the data into two groups (clusters).
I propose that we modify some parameters to practice with the tool before moving forward. For example, we can modify some parameters with a learning rate of 0.03 and a ReLU activation function (the regularization is not going to be used since it is outside the scope of this book).
We maintain the problem as classification, and I propose that we put the “ratio of training-to-test” to 50% of the data and that we also keep the “noise” parameter to zero to facilitate the visualization of the solution (although I suggest that later you practice with it on your own). We can leave the “batch size” at 10.
And, as before, we will use “X1” and “X2” for the input. I suggest starting with a single hidden layer with a single neuron. We can achieve this by using the “-” or “+” buttons:
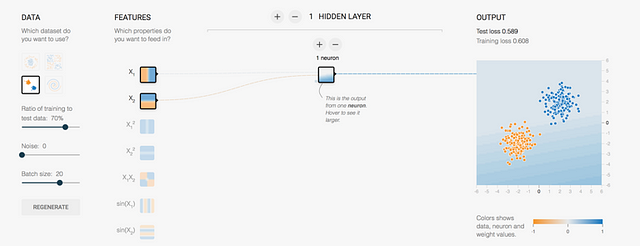
In the upper right, we see that the initial values of the “Test loss” and “Training loss” are high (the reader can get different values since the initial values are generated in a random way). But after pressing the “play” button, it can be seen that both the “Training loss” and the “Test loss” converge at very low ratios and remain the same. Moreover, in this case, both lines, black and gray, perfectly overlap.
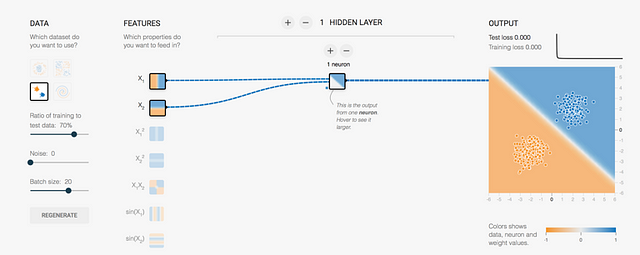
Classification with more than one neuron
Let’s choose another set of starting data like the one in the attached figure:

We now want to separate the two datasets: the orange ones must be classified in one group and the blue ones in another. But the problem is that in this case they will have a circular shape where the orange points will be in the outer circle and the blue points will be inside. Now, these points cannot be separated with a single line as before. If we train with a hidden layer that has a single neuron as the model of the previous classification, the classification will fail in this case.
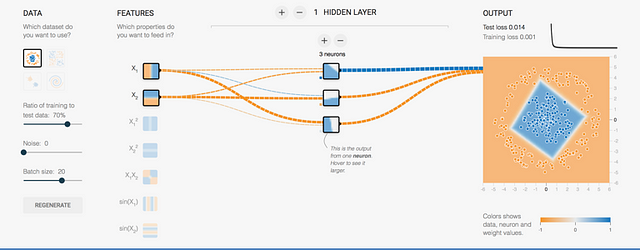
I suggest that we test with multiple neurons in the hidden layer. For example, try two neurons: you will see that you have not tuned enough yet. I propose that you then try with three. You will see that, in the end, you can get a much better training and test loss:
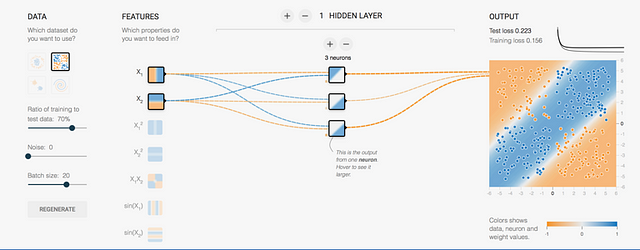
Let’s go for another of the datasets on the left, that where the data is divided into four different square zones. Now, this problem cannot be solved with the previous network, but I propose that you try it:
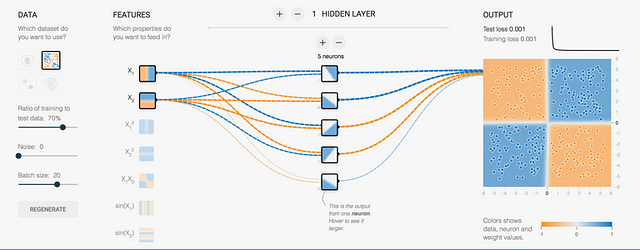
As can be seen, we are not able to get a good classification (although in some cases it could happen that with only 3 neurons it works since the initialization is random, but if you do several tests you will see that it is not achieved in general). However, if we have 5 neurons as in the following figure, the reader can see how this neural network gets a good classification for this case:
Classification with several layers
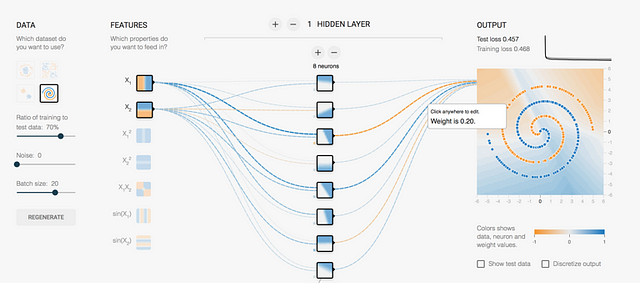
Now we will try to classify the dataset with the most complex pattern that we have in this tool. The swirling structure of the orange and blue data points is a challenging problem. If we rely on the previous network, we see that not even having 8 neurons, the maximum that the tool leaves us, we get a good classification result:
If the reader has tried it, in this case I suppose that you will get a few good values for the test loss. The time has come to put more layers; I assure you that, if you use all the layers the tool allows, you will get it:
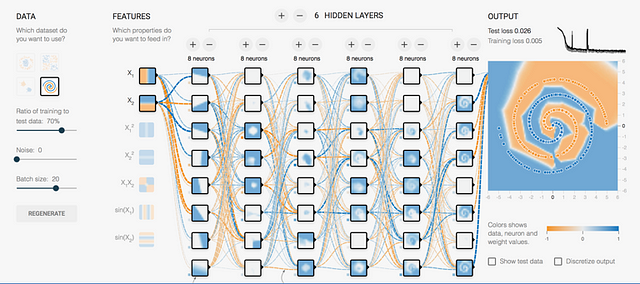
But you will see that, as it is obvious, the process of learning the parameters takes a long time.
Actually, with fewer layers or neurons you can get good results; I challenge you to play a little on your own, also changing for example the activation functions to get a simpler model. You can also consider testing any other parameter.
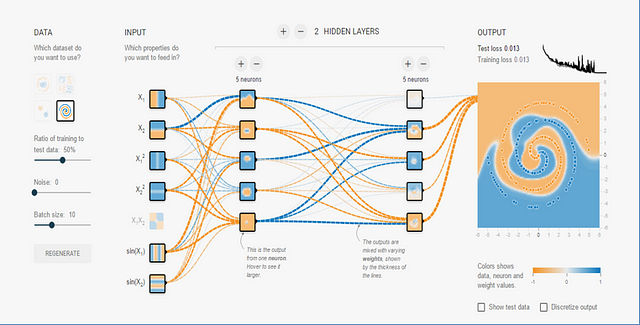
This tool only considers dense neural networks; later we will see that the convolutional neural networks (and the recurrent neural networks) present more complex dilemmas. But only with these dense networks can we see that one of the most difficult hyperparameters to adjust is to decide how many layers the model has and how many neurons each of these layers has.
Using very few neurons in the hidden layers will result in what is called underfitting, a lack of fit of the model because there are very few neurons in the hidden layers to properly detect the signals in a complicated dataset.
On the other hand, using too many neurons in the hidden layers can cause several problems. First, it can produce overfitting, which occurs when the neural network has so much information processing capacity that the limited amount of information contained in the training set is not enough to train all the neurons in the hidden layers. But on the other hand, a large number of neurons in the hidden layers can increase the time needed to train the network to the point that it is impossible to properly train the neural network in the necessary time.
Obviously, we must reach a compromise between too many and very few neurons in the hidden layers and that is why I have already commented that we are facing a challenge that requires more art than science.
I hope that this post have been helpful and you will use them at work or in college. Soon the next one!